Facts for Kids

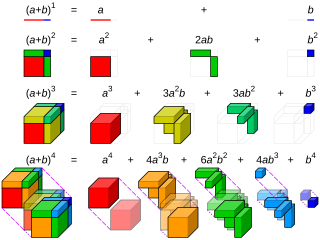
The Binomial Theorem helps us understand how to expand expressions like (a + b)ⁿ. It tells us how many ways we can choose different parts of our expression! For example, if we have (x + 2)³, we can find the result by multiplying it out. The theorem was discovered by mathematicians like Sir Isaac Newton and Blaise Pascal. 📚✨ It has cool applications in algebra, probability, and even in games! The theorem lets us work with powers in a simpler way and is super important for anyone who loves math. Let’s explore this fascinating topic! 🎉

A common misconception about the Binomial Theorem is thinking that it only works for whole numbers! 🛑

However, it works for fractions and even negative numbers too! Another misunderstanding is that students may confuse coefficients with terms. Remember: coefficients are the numbers in front, while terms are parts of the expression. Lastly, some might think it only applies in math class, but it’s everywhere in real life! 🌍

Understanding these differences helps clarify how useful the Binomial Theorem is in many situations! Let’s bust those myths together! 💪

Let’s practice with the Binomial Theorem! 📘

For instance, expand (x + 3)². First, identify the coefficients from Pascal's Triangle: 1, 2, 1. So, (x + 3)² = 1(x²) + 2(3x) + 1(3²) = x² + 6x + 9! 🎉

Now, try expanding (y + 4)³. Remember, you can use the coefficients: 1, 3, 3, 1! Find the result and see how you did! Lastly, practice spotting coefficients in a few different expressions to get familiar with them. Math is a journey, and practicing helps us learn! 🚀

If you want to learn more about the Binomial Theorem, there are many fun resources! 🌟

You can read "Algebra for Kids" by William Dunham or explore online videos on math websites like Khan Academy! 📹

Websites like Coolmath4kids.com also have fun games and explanations. Libraries have books on math history, like "Mathematics: A Very Short Introduction" to see how the theorem fits into the bigger picture. Don’t forget to ask your teacher any questions you have! 📚

Exploring math is a wonderful adventure full of discoveries! Happy learning! 🎈

To prove the Binomial Theorem, we can use mathematical induction! 🤔

This means showing that if it's true for one number, it also holds for the next. First, we check that it works for n=1. Then, we assume it’s true for n=k and show it works for n=k+1. This involves rearranging terms and using coefficients from Pascal's Triangle. The exciting part is that this method confirms that each term in the expansion follows the pattern in the Binomial Theorem! Math can be like a puzzle sometimes, and proving theorems is one of its coolest parts! 🧩

The history of the Binomial Theorem goes back thousands of years! 📜

One of the earliest records was in ancient China, around 200 BC, where mathematicians explored similar ideas. However, it was Sir Isaac Newton in the 17th century who really made it famous! He published his findings in 1665. 🙌

Blaise Pascal, from France, created Pascal's Triangle, which helps find the coefficients (the numbers in front of each term) in the expansions. Today, we owe a lot to these clever mathematicians who helped us understand this theorem that is still used in classrooms worldwide! 🌎

Binomial coefficients are special numbers that show how many ways we can choose items from a group! 🧮

In the expression (a + b)ⁿ, the coefficients are found in Pascal's Triangle. For example, in (x + 2)³, the coefficients are 1, 3, 3, and 1. These tell us how many of each term there are when we expand the expression. The nth row in Pascal's Triangle shows the coefficients for (a + b)ⁿ. Understanding these helps us become better at solving math problems and understanding patterns! 🌟

The Binomial Theorem has amazing applications! 🎨

In probability, it helps calculate chances of events happening. For example, if you're flipping a coin, the theorem helps find the probability of getting heads or tails a certain number of times. 🎲

It’s also used in computer science for algorithms and coding. Plus, artists use it to create designs and patterns! The theorem is not just for math class; it appears in real life when you bake too! 🍰

If you mix different ingredients, the Binomial Theorem helps figure out how they combine!

There are many generalizations of the Binomial Theorem! 🤯

One cool one is the Binomial Series, which is used when we have powers that aren't whole numbers. This helps in more advanced math, like calculus. Calculus is the study of change and motion! Another generalization involves negative and fractional exponents, which also expand using the Binomial Theorem rules. These ideas are super useful for math wizards who want to tackle even more complex problems! 🌈

This shows us how the Binomial Theorem grows and connects to other branches of mathematics.